问题描述
这个问题源于以夫拉维·约瑟夫(他是一世纪时的著名历史学家)命名的古老问题,但稍有变化。传说如果不是由于他的数学天赋,约瑟夫不会活到出名的那一天。在犹太罗马战争期间,他们41名犹太反抗者困在了罗马人包围的洞穴中。这些反抗者宁愿死也不愿被活捉,于是决定围成一个圆圈,并沿着圆圈每隔两个人杀死一个人,直到剩下最后两个人为止。但是,约瑟夫和一个未被告发的同谋者不希望无畏的自杀,于是他迅速计算出他和其朋友在这个险恶的圆圈中应该站的位置。
我们这个问题略有变化,从围成标有记号1到n的圆圈的n个人开始,每隔m个删去一个人,直到只有一个人幸存下来。例如m=2,n=10的起始图形:
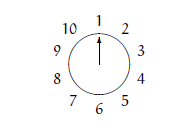
消去的顺序是2,4,6,8,10,3,7,1,9,于是5幸存下来,所以J_{2}(10)=5。问题:确定幸存者 J_{m}(n).下面给出的程序代码都是给定输入n,m给出J_{m}(n)。
方法一:链表模拟
该方法虽然笨拙(一般都超时,这里有个提交不超时的地方),但是相当简单,具体实现代码如下:
#define _CRT_SECURE_NO_WARNINGS
#include<iostream>
#include<list>
using namespace std;
list<int> cycle;
int fun(int n,int m)
{
int k = 1; cycle.clear();
for (int i = 1; i <= n; ++i)cycle.push_back(i);
list<int>::iterator b = cycle.begin();
while (cycle.size() != 1) {
if (k++ == m) b = cycle.erase(b), k = 1;
else ++b;
if (b == cycle.end()) b = cycle.begin();
}
return *(cycle.begin());
}
int main()
{
ios::sync_with_stdio(false);
int n, m;
cin >> n >> m;
cout << fun(n, m) << endl;
return 0;
}
方法二:递归方程
应用递归方程解封闭形式可以很容易求解m=2的情况,在这种情况下:
我们假设一开始有2n个人,经过一轮后剩下的是:
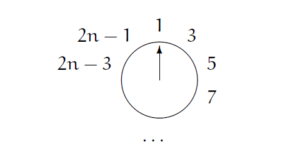
3号就是下一个要离开的人,除了每个人的号码加倍并减去1之外,这正像对n个人开始时的情形,也就是说:
J(2n) = 2J(n) - 1 ,\quad n \geq 1由此,我们得到了一个非常有用的结论,进一步的,当一开始有2n+1个人的时候,经过一轮后剩下的是:
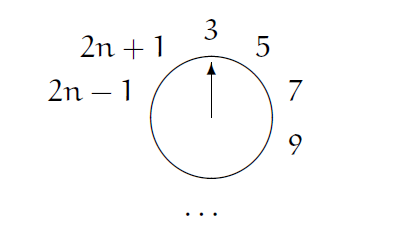
同理,我们可以得到如下的结论:
J(2n+1) = 2J(n) + 1 ,\quad n \geq 1将这些方程和J(1)=1组合起来,我们得到:
\begin{alignedat}{1}
J(1)&=1 \\
J(2n) &= 2J(n) - 1 ,\quad n \geq 1 \\
J(2n+1) &= 2J(n) + 1 ,\quad n \geq 1
\end{alignedat}然后解出这个递推式就可以了,具体方法参见具体数学-使用成套方法解递归式
方法三:动态规划
具体可以参考:数论三·约瑟夫问题。具体代码如下:
#define _CRT_SECURE_NO_WARNINGS
#include<iostream>
using namespace std;
int main()
{
ios::sync_with_stdio(false);
int n, m, r = 0;
cin >> n >> m;
for (int i = 2; i <= n; ++i) r = (r + m) % i;
cout << r+1 << endl;
return 0;
}
方法四:数学方法
具体来说也是动态规划,不过是从具体数学中看到的,就称为数学方法吧!具体拿m=3来说,这个方法的思想是,只要有一个人被处死,我们就定义新的号码。这样一来,1号和2号就会变成n+1和n+2,然后3号被处死,依次类推,3k + 1号和3k+2号就会变成n+2k+1和n+2k+2.例如n=10,m=3的号码如下

最后一个被处死的是3n,所以我们只要能算出3n原来的号码就可以了!
#define _CRT_SECURE_NO_WARNINGS
#include<iostream>
using namespace std;
int main()
{
ios::sync_with_stdio(false);
long long int n, m; cin >> n >> m;
long long int N = n * m;
while (N > n) N = (N - n - 1) / (m - 1) + N - n;
cout << N << endl;
return 0;
}